摘要
当用户在搜索引擎上查询感兴趣的条目时,通常得到一个包含相关网页链接的列表。用户从第一个网页链接开始,浏览所有的感兴趣的链接并点击,直至得到想要的结果或者是最后一个链接为止。这种用户浏览行为称为dependent click model(DCM)。论文通过最大化推荐的网页链接推荐满意度,向用户推荐最合适的网页链接。在此报告中,先介绍与论文相关的多臂赌博机问题(multi-armed bandit problem)。然后介绍论文作者在2015年发表的相关论文《Cascading Bandits: Learning to Ranking the Cascade Model》,论文与DCM是类似的。最后是DCM的介绍。
参考资料
- https://zhuanlan.zhihu.com/p/21388070 专治选择困难症——bandit算法
- http://banditalgs.com/2016/09/18/the-upper-confidence-bound-algorithm/ The Upper Confidence Bound Algorithm
- Kveton B, Szepesvari C, Wen Z, et al. Cascading Bandits: Learning to Rank in the Cascade Model[C]// ICML. 2015:767-776.
- Katariya S, Kveton B, Szepesvári C, et al. DCM Bandits: Learning to Rank with Multiple Clicks[J]. 2016.
介绍
搜素引擎通常把推荐的网页链接进行排序,按照相关度来进行排序,最相关的网页放在最前面方便用户浏览。在推荐中往往会考虑用户点击的数据,比如cascade mode(Craswell et al., 2008)是网页搜索中最流行的用户行为模型之一。在2015年,本论文的作者曾提出在线的遗憾优化学习算法(regret-optimal online learning algorithms),此级联模型的主要限制在于不能学习多次点击的行为。
在论文中作者提出一个在线学习的算法DCM来学习用户多次点击的问题。在每一个时刻t,推荐给用户一个包含K个网页链接的列表,用户从最开始的链接浏览至最后一个链接,当用户找到感兴趣的链接时会点击链接并且浏览网页,然后可能会离开搜索的界面或者继续浏览下一个链接。当用户离开搜索的界面时,DCM会判断用户是否已经得到其想要的信息:如果用户得到想要的结果离开搜索界面,DCM会得到奖励1;如果用户浏览所有的链接并得不到满意的结果,DCM得到奖励0。DCM的目标在于最大化总的奖励,或者说最小化累积遗憾(推荐的K个网页链接和最优的推荐结果间的差异累积)。本论文中的一个挑战是用户是否得到满意结果是未知的。
在此阅读报告中,着重介绍论文的思想和做法,对于公式的推导过程不做详细的介绍。
多臂赌博机
多臂赌博机问题(multi-armed bandit problem),与平常生活中遇到各式各样的选择问题是息息相关的。比如:去哪里上大学、选择什么专业、中午吃什么等。为此解决这问题需要进行有策略的进行选择,而这就是bandit算法。其解决的问题如下:
一个赌徒,要去摇老虎机,走进赌场一看,一排老虎机,外表一模一样,但是每个老虎机吐钱的概率可不一样,他不知道每个老虎机吐钱的概率分布是什么,那么想最大化收益该怎么整?这就是多臂赌博机问题。怎么解决这个问题呢?最好的办法是去试一试,而这个试一试也不是盲目地试,而是有策略地试,越快越好,这些策略就是bandit算法。

多臂赌博机问题和很多问题之间是有联系的:1. 假设一个用户对不同类别的内容感兴趣程度不同,那么我们的推荐系统初次见到这个用户时,怎么快速地知道他对每类内容的感兴趣程度?这就是推荐系统的冷启动;2. 假设我们有若干广告库存,怎么知道该给每个用户展示哪个广告,从而获得最大的点击收益?是每次都挑效果最好那个么?那么新广告如何才有出头之日? 3. 我们的算法工程师又想出了新的模型,有没有比A/B test更快的方法知道它和旧模型相比谁更靠谱?以下本文主要介绍解决此问题的UCB算法。
### 问题描述
假设有K个老虎机排列在面前,每一次我们可以选择一个老虎机来按并且获得奖励。但老虎机的选择有两个问题:是应该选择过去回报率高的老虎机,还是选择过去回报率较低但是有潜力的老虎机呢?对此,我们可以假设K个老虎机的奖励独立服从一个概率分布,记录每一轮中老虎机的奖励信息,根据历史信息选择奖励最高的老虎机。在多臂赌博机中,把老虎机称之为臂。
### UCB算法
这个算法被认为是乐观面对不确定性:首先每一轮猜测各个臂可能给出的奖励,然后选择奖励最高的臂,如果实际获得的奖励少则减少臂的奖励估计,减少对臂的选择;否则提高臂的奖励估计,增加对臂的选择。里面对臂的奖励估计,则是建立一个指数,通过动态的调整指数参数来对臂的奖励估计。
所以需要一个定义策略好坏的指标——累积遗憾:一个策略A和一个动作集{K},在T时间后的累积遗憾是策略A的期望奖励和最佳臂的期望奖励之差。
定义策略的奖励为$f(A)$,则最优臂为$A^{\ast}=arg \max \limits_{A\in{K}}f(A)$,所以策略A的累积遗憾$R_T(A)=f_T(A^{*})-f_T(A)$,表示该策略与收益期望最大的臂之间的收益差异。所以一个好的策略应该是最小化:
$$R(n)=E\left[\sum_{i=1}^n\left[R_t (A_t)\right]\right ]$$
定理:假设$X_1,X_2,…,X_n$相互独立且服从1-次高斯分布(方差为1、均值为0),$u ̂=\sum_{t=1}^n X_t/n$,可以得到$P(u ̂≥ε)≤exp(-\frac{nε^2}{2})$。
可以写作:$P(u ̂≥\sqrt{\frac{2}{n} log(\frac{1}{δ}))}≤δ$。
所以,对于某个老虎机的估计,可能的形式为:$\hat{u}_i (t-1)+\sqrt{\frac{2}{T_i (t-1)} log(\frac{1}{δ})}$。
δ的选择不同产生不同的算法,当δ越小,策略的选择越乐观(因为指数变得更大)。
UCB算法的具体算法如下:取δ=1/t,t是试验的总次数
>1. 对每个臂先试一次观察收益情况;
>2. 以后每次选择指数最大的臂$\hat{u}_i (t-1)+\sqrt{2/(T_i (t-1)) log(t)}$。
UCB算法的累积期望遗憾是$O(logN)$,最坏情况下累积遗憾不超过$O(\sqrt{KNlogN})$。
## Cascading Bandits: Learning to Ranking the Cascade Model
此论文是阅读论文的作者2015年写的,相当于是一个简化版本。
对于用户搜索的条目,搜索引擎返回推荐的K个网页链接,通常K个网页链接是按照相关性进行排序的。用户通常从第一个网页链接浏览到最后一个链接,然后选择最感兴趣的链接进行点击浏览。基于这种用户行为,论文中为了解决搜索引擎中的推荐问题,提出了两个模型:CascadeUCB1和CascadeKL-UCB。两个模型的差异在于置信上限的计算不同。
而且论文中的设定的用户行为模式与现实具有差异的,所以模型不能解决多次点击的行为。
### 用户行为模式
用户的行为模式如下图所示:
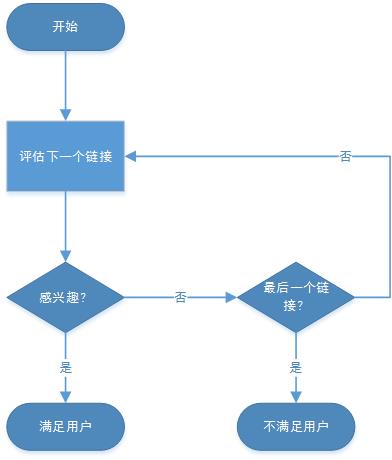
### 算法
假设总共有n个网页链接,每次向用户推荐K个链接。在第t步得到的奖励认为是推荐的K个网页至少有一个被点击的概率:
$$f(A,w)=1-\prod_{k=1}^K(1-w(a_k ))$$
其中$A=(a_1,…,a_K)$和$w∈[0,1]^E$。
所以累积遗憾函数的计算为$R(A_t,w_t )=f(A^{\ast},w_t )-f(A_t,w_t)$,$A^{\ast}=arg\max \limits_{A∈∏_K(E)}f(A,\overline w)$为理想的网页。
具体的算法步骤如图所示,思想是和多臂赌博机的类似的:

>1. $w_0\sim P$: $w_t (e)∈{0,1}$表示用户在时间t对链接e的偏好程度。这个偏好是随机的并且服从伯努利分布(用户感兴趣的链接均值为$p$,不感兴趣的链接均值为$p-\Delta$);
>2. $∀e∈E:T_0 (e)←1$:相当于每个链接首先推荐一遍并被浏览;
>3. $∀e∈E:w ̂_1 (e)←1$:每个链接预设浏览了一次并被点击;
>4. Compute UCBs:计算每个链接的置信上限;
>5. $A_t←(a_1^t……a_K^t)$:选取置信上限最大的K个网页链接进行推荐;
>6. $C_t∈{1,…,K,∞}$:表示用户浏览的终止位置,当C_t≤K表示用户找到感兴趣的链接,当C_t=∞表示用户浏览了所有的链接没有找到感兴趣的;
>7. $T_t (e)←T_{t-1} (e)+1$:表示链接被浏览的次数加一;
>8. $w ̂_{T_t (e) } (e)←⋯$:更新浏览过的链接被点击的次数。
与原先的多臂赌博机问题相比,可以看出计算过程是相似的。每一次像用户推荐K个链接,用户浏览了前$C_t≤K$个链接,并且点击了第$C_t$个链接。可以把每个链接看做是一个赌博机,按照置信上限从大到小向用户逐个推荐链接,并且得到一个收益(用户满不满意),而${C_t+1,…,K}$的链接没有进行试验。由此看来,与原先多臂赌博机问题的差异在于UCBs的计算。
CascadeUCB1算法中:$U_t (e)=\hat{w}_{T_{t-1}(e) ) } (e)+\sqrt{\frac{1.5}{T_{t-1}(e) } log(t-1)}$,与多臂赌博机相比只是系数上的差异;CascadeKL-UCB算法中:$U_t (e)=\max\left\{q\in\left[\hat{w}_{T_{t-1}(e)} (e),1\right]:T_{t-1} (e) D_{KL} \left(\hat{w}_{T_{t-1}(e) } \left(e\right)||q\right)\leq logt+3loglogt\right\}$,其中$D_{KL}(p||q)$是两个服从均值为p和q的伯努利分布变量的KL散度,这里是找一个最大的置信上限满足和观测的均值差异在一个区间内。
## DCM Bandits: Learning to Rank with Multiple Clicks
上篇论文中,用户的行为假定只点击一个最吸引他的网页。而在实际情况中,用户往往是点击多个感兴趣的页面,当浏览到需要的网页或者不存在感兴趣的网页才终止浏览的行为。论文中假设每个网页对用户的吸引概率是独立的,并且用户在浏览网页后有个终止的概率表示获取到需要的网页。用户依次浏览推荐的K个网页,用户会点击吸引他的网页,当用户点击网页浏览后如果获取到需要的信息则终止浏览,否则继续浏览下一个网页。为此论文中提出了dcmKL-UCB模型。
### 用户行为模式
与上一个模型相比,用户会点击多个链接,并且在每一个链接中有一定的概率离开。
用户行为模式如下图所示:
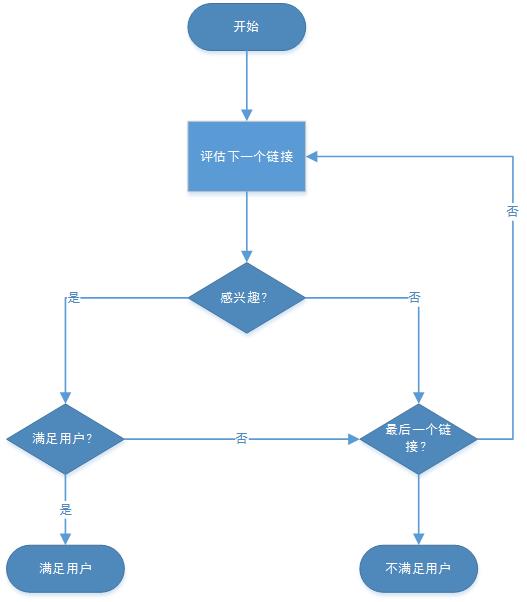
算法
论文中新增添一个只和位置k相关的终止概率,表示当用户在浏览第k个链接后终止继续浏览的概率。当存在一个网页链接是吸引用户的,可以看作收益为1,即$w(e)=1$且$v(k)=1$。所以在第t步得到的奖励认为是推荐的K个网页至少有一个满足用户的需求的概率
$$
f(A,w,v)=1-\prod_{k=1}^K\left(1-v(k)w(a_k )\right)
$$


实验
算法中预设参数:
- 总网页链接数L;
- 用户感兴趣的网页链接数K,假设编号为0——K-1;
- 用户感兴趣的网页,吸引概率p=0.2;
- 用户不感兴趣的网页与感兴趣的网页之间的吸引用户概率的gap为∆,所以不感兴趣的网页吸引用户的概率为p-∆;
- 每个位置的终止概率为γ=0.8。
- 总的迭代次数n=10^5;
每组实验做20次,取均值作为实验结果。

实验结果可以得出:
- 期望累积遗憾随着K的增大而减少;
- 期望累积遗憾随着L的增大而变大;
- 期望累积遗憾随着∆的减少而变大。