摘要
论文中提出BanditNet模型,能够利用bandit feedback数据,即实体标签服从某个分布的数据,能够有效地使用大量的数据训练已有的模型使之达到很好的效果。并且模型只需要较少的代价对模型重训练,能够达到全部数据的效果。论文中采用图像是别的数据验证模型效果,并不是传统意义上的有标签图像,其中图像的标签可能会发生变化。
参考资料
- Joachims T, Swaminathan A, de Rijke M. Deep learning with logged bandit feedback[J]. 2018.
- Swaminathan A, Joachims T. The self-normalized estimator for counterfactual learning[C]//advances in neural information processing systems. 2015: 3231-3239.
介绍
在推荐系统中,后台中的log数据通常能够反映系统的性能以及用户的浏览经历,如广告投放系统中包括广告投放数据和用户是否点击数据。但每一个数据是通过系统产生展示实体给用户,用户对实体的行为反馈产生了数据。其中系统的推荐行为只是所有可能行为中的子集,所以得到用户反馈是由推荐系统所直接影响,这叫做bandit feedback。由和传统的有监督学习不同的在于我们不知道所有行为的真实反馈,即用户在其它实体上的行为反馈。论文中的目的是在bandit feedback数据上进行训练,即使不是在全部数据上进行训练,也能够得到很好的效果。
假设输入$x \in \mathcal{X}$,服从一个未知的分布$\operatorname{Pr}(\mathcal{X})$。输出假设为$y \in \mathcal{Y}$,其中$y$服从条件概率分布$\pi_{w}(Y | x)$。输入和动作之间也会有一个得分反馈$\delta(x, y)$。通俗来讲,在推荐系统中,$x$可以表示为用户和浏览网页,$y$表示展示的广告,$\delta(x, y)$当用户点击广告时为1否则为0,$\pi_{w}(Y | x)$即推荐系统基于用户和网页信息计算得出的广告推荐的概率分布。简单的,每个动作$y$的推荐概率可以用softmax的形式表达:
$$\pi_{w}(y | x)=\frac{\exp \left(f_{w}(x, y)\right)}{\sum_{y^{\prime} \in \mathcal{Y}} \exp \left(f_{w}\left(x, y^{\prime}\right)\right)}$$
因此一般情况下,系统的学习目标在于找到最好的策略$\pi_{w}$最大化收益,即最大化点击率等:
$$R\left(\pi_{w}\right)=\underset{x \sim \operatorname{Pr}(X)}{\mathbb{E}}\underset{ y \sim \pi_{w}(Y | x)}{\mathbb{E}}[\delta(x, y)]$$
但训练的数据都是经过原先的推荐策略$\pi_{0}$采样得到,即$y \sim\pi_{0}$,由于$\pi_{w}\neq \pi_{0}$,不能直接代入数据优化$R\left(\pi_{w}\right)$。
重新修正$y$的分布,可以得到以下的目标期望:
$$R\left(\pi_{w}\right)=\underset{x \sim \operatorname{Pr}(X)}{\mathbb{E}}\underset{ y \sim \pi_{w}(Y | x)}{\mathbb{E}}[\delta(x, y)]=\underset{x \sim \operatorname{Pr}(X)}{\mathbb{E}}\underset{ y \sim \pi_{0}(Y | x)}{\mathbb{E}}\left[\delta(x, y)\frac{\pi_{w}(y | x)}{\pi_{0}(y | x)}\right]$$
通过历史推荐策略$\pi_{0}$产生的数据,优化目标函数:
$$\hat R_{I P S}\left(\pi_{w}\right)=\frac{1}{n} \sum_{i=1}^{n} \delta_{i} \frac{\pi_{w}\left(y_{i} | x_{i}\right)}{\pi_{0}\left(y_{i} | x_{i}\right)}$$
但公式中存在着倾向性过拟合(propensity overfittin)的问题。在$R\left(\pi_{w}\right)$中发生一个偏移,和得分反馈$\delta(x, y)$发生偏移在期望计算中是结果是相同的,使得期望发生线性偏移。但事实上,$\hat R_{I P S}$的计算和期望的不一样:
$$c+\min_{w} \frac{1}{n} \sum_{i=1}^{n} \delta_{i} \frac{\pi_{w}\left(y_{i} | x_{i}\right)}{\pi_{0}\left(y_{i} | x_{i}\right)} \neq \min_{w} \frac{1}{n} \sum_{i=1}^{n}\left(\delta_{i}+c\right) \frac{\pi_{w}\left(y_{i} | x_{i}\right)}{\pi_{0}\left(y_{i} | x_{i}\right)}$$
算法优化的过程中更关注低概率的$\pi_{0}\left(y_{i} | x_{i}\right)$。所以优化目标会收到历史推荐策略的影响,而不仅仅是实际动作。
采用self-normalized IPS estimator的方式,可以将目标函数转化为:
$$\hat R_{S N I P S}\left(\pi_{w}\right)=\frac{\frac{1}{n} \sum_{i=1}^{n} \delta_{i} \frac{\pi_{w}\left(y_{i} | x_{i}\right)}{\pi_{0}\left(y_{i} | x_{i}\right)}}{\frac{1}{n} \sum_{i=1}^{n} \frac{\pi_{w}\left(y_{i} | x_{i}\right)}{\pi_{0}\left(y_{i} | x_{i}\right)}}$$
这里相当于对已有的进行归一化权重,和之前的相比效果更精确。并且容易得知当发生偏移$\delta_{i}+c$时,$\hat R_{S N I P S}\left(\pi_{w}\right)$同样也会有偏移$c$,因此目标函数和反馈之间是等变化的。
记$S:=\quad \frac{1}{n} \sum_{i=1}^{n} \frac{\pi_{w}\left(y_{i} | x_{i}\right)}{\pi_{0}\left(y_{i} | x_{i}\right)}$,当数据样本趋向于无穷大时,容易得知$S$会趋向$1$:
$$\mathbb{E}[S]=\frac{1}{n} \sum_{i=1}^{n} \int \frac{\pi_{w}\left(y_{i} | x_{i}\right)}{\pi_{0}\left(y_{i} | x_{i}\right)} \pi_{0}\left(y_{i} | x_{i}\right) \operatorname{Pr}\left(x_{i}\right) d y_{i} d x_{i}=\frac{1}{n} \sum_{i=1}^{n} \int 1 \operatorname{Pr}\left(x_{i}\right) d x_{i}=1$$
假设$S=1$代入,并且采用拉普拉斯乘子加入限制的条件:
$$L(w, \lambda)=\frac{1}{n} \sum_{i=1}^{n} \frac{\delta_{i} \pi_{w}\left(y_{i} | x_{i}\right)}{\pi_{0}\left(y_{i} | x_{i}\right)}-\lambda\left[\frac{1}{n}\left(\sum_{i=1}^{n} \frac{\pi_{w}\left(y_{i} | x_{i}\right)}{\pi_{0}\left(y_{i} | x_{i}\right)}\right)-S_{j}\right]=\frac{1}{n} \sum_{i=1}^{n} \frac{\left(\delta_{i}-\lambda\right) \pi_{w}\left(y_{i} | x_{i}\right)}{\pi_{0}\left(y_{i} | x_{i}\right)}+\lambda S_{j}$$
如公式所示,$S_j$是枚举的$\quad \frac{1}{n} \sum_{i=1}^{n} \frac{\pi_{w}\left(y_{i} | x_{i}\right)}{\pi_{0}\left(y_{i} | x_{i}\right)}$大小,通过超参$\lambda$控制权重。事实上由于$S$趋向1,程序中的实习是设定$S_j=1$,所以最后目标函数只是得分反馈减去超参$\lambda$。
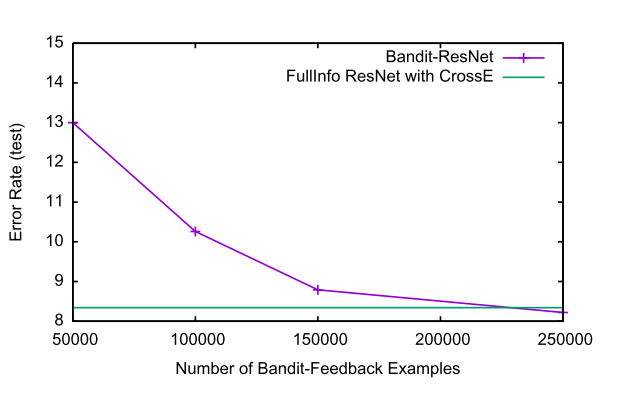
实验结果中表明,利用bandit feedback的数据进行训练也能得到和全部数据一起训练的效果。
感想
这篇论文中,其实很多细节我都没有弄的很清楚。但是能够帮我去理解,推荐系统如何利用新的数据进行增量学习,有比较好的启发。